Overview
SQISign is an isogeny-based signature scheme that exploits the Deuring correspondence, which connects the world of supersingular elliptic curves over $\mathbb{F}_{p^2}$ to the world of quaternion algebras. More precisely, we have a one-to-one map between the following objects:
- Supersingular $j$-invariants over $\mathbb{F}_{p^2}$ (up to Galois conjugacy) $\leftrightarrow$ Maximal orders in $\mathcal{B}_{p, \infty}$ such that $\OO \cong \text{End}(E)$ (up to isomorphism).
- An isogeny $\varphi: E \rightarrow E_1$ of degree $D$ $\leftrightarrow$ an integral left $\OO$-ideal and right $\OO_1$-ideal $I_{\varphi}$ of norm $n(I_\phi) = D.$
- An endomorphism $\theta \in \text{End}(E_0)$ $\leftrightarrow$ A principal ideal $\OO \cdot \theta$.
If we have two isogenies $\varphi: E \rightarrow E_1$ and $\psi: E \rightarrow E_1$ (i.e., two isogenies with the same domain and codomain), they will correspond to equivalent ideals $I_{\varphi} \sim I_{\psi}$. This correspondence also behaves well with multiplication of ideals. Namely the ideal $I_{\rho} \cdot I_{\tau}$ is equal to $I_{\tau \circ \rho}$ and therefore corresponds to the isogeny $\tau \circ \rho$.
Developing efficient algorithms for the maps translating objects to and from the geometric world of elliptic curves and algebraic world of quaternions has been the focus of many works, including for example [KLPT14], [GPS17], [EHLMP18], [DKLPW20], [W21], [DLW22], and [EPSV23].
- Given a $j$-invariant $j(E)$, it is computationally hard to compute the corresponding maximal order as this would require the computation of the endomorphism ring of $E$, which is conjectured to be a hard problem. In fact, this underlies the security of isogeny-based cryptography. Indeed, the quaternion $\ell$-isogeny problem, which is the analogue of the $\ell$-isogeny problem in quaternion algebras, can be solved in polynomial time ( and ) conversely, given the maximal order $\OO$, it is easy to compute the corresponding supersingular elliptic curve.
- By following the $\textsf{IdealToIsogeny}$ and $\textsf{IsogenyToIdeal}$ algorithms introduced in the SQISign paper, we are able to implement efficient algorithms for the translation of ideals to and from isogenies.
SQISign is obtained from a high-soundness, one round interactive identification protocol by the Fiat-Shamir transform. In our code, we implement this identification protocol, as described in the original paper, which consists of the following algorithms:
Setup: on input of the security parameter $\lambda$, pick a suitable prime number $p$ and let $E_0: y^2 = x^3 + x$ be the special supersingular curve over $\mathbb{F}_{p^2}$. Throughout, we will fix $p \equiv 3 \bmod 4$. Then, select an odd, smooth, $\lambda$-bit numbers $D_c, T’$ with $\gcd(D_c, T’) = 1$ which divide $(p^2 - 1)$. Let $D = 2^e$, where $e$ is greater than the diameter of the $2$-isogeny graph.Keygen: given parameters, pick a random isogeny $\tau: E_0 \rightarrow E_A$ of prime degree $N_{\tau}$, leading to a random elliptic curve $E_A$. The public key is $E_A$ and the secret key is the isogeny $\tau$.Commitment: the prover generates a random (secret) isogeny walk $\psi: E_0 \rightarrow E_1$ of degree $T’$ and sends $E_1$ to the verifier.Challenge: the verifier sends the degree-$D_c$ cyclic isogeny $\varphi: E_1 \rightarrow E_2$ to the prover.Response: from $\varphi \circ \psi \circ \widehat{\tau}: E_A \rightarrow E_2$, the prover constructs a new isogeny $\sigma: E_A \rightarrow E_2$ of degree $D$ with $\widehat{\varphi}\circ \sigma$ cyclic, and sends $\sigma$ to the verifier.Verify: the verifier accepts the response if $\sigma$ is a degree-$D$ isogeny from $E_A$ to $E_2$ and the isogeny $\widehat{\varphi}\circ \sigma : E_A \to E_1$ is cyclic. If any of these conditions are not met, the verifier rejects the response.
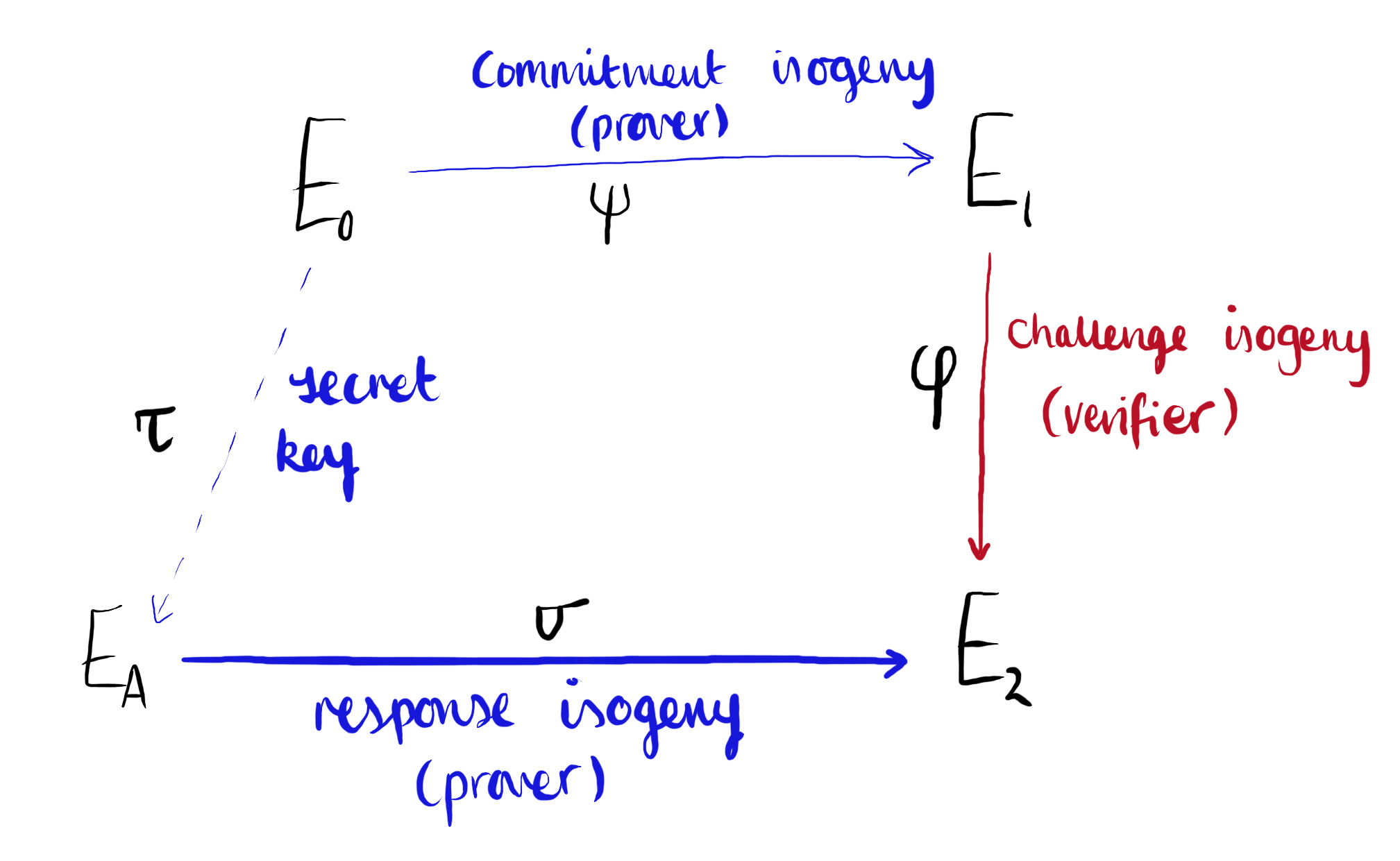
Figure 1: The SQISign Identification Protocol. Diagram inspired by Figure 1 in the original SQISign paper
We now discuss these in more depth.
Setup
We implement this in setup.py, which computes all the global variables needed for the various algorithms given parameter sets designed for SQISign in parameters.py.
In the parameters file, we currently have two parameters sets from which to chose: a toy $54$-bit prime $p_{\text{toy}}$, for which SQISign takes around 30 seconds to run; and a cryptographic sized $256$-bit prime $p_{6983}$ which terminates in around 12 minutes at the time of writing.
The remaining algorithms (from key generation to verification) can all be found in SQISign.py.
Key generation
Note: We implement the efficient alternative key generation as described in Appendix D of the SQISign paper:
- Select a prime $N_{\tau} \leq B_{\tau} \simeq p^{1/4}$ that is inert in $\mathbb{Z}[i]$ uniformly at random (note that this is specific to $p \equiv 3 \bmod 4$; otherwise we require it to be inert in $\mathbb{Z}[\omega]$, the ring of integers of $\mathcal{B}_{p, \infty}$).
- Compute an endomorphism $\gamma \in \OO_0$ of norm $N_{\tau} \ell^{e_\tau}$, where $e_{\tau} \approx \log(p)$, by running $\textsf{RepresentInteger}_{\OO_0} (N_{\tau} \ell^{e_\tau})$.
- Set $I_{\tau} = \OO_0 \gamma + \OO_0 N_{\tau}$, which will be an integral left $\OO_0$-ideal of prime norm $N_{\tau}$.
- Set $J_{\tau} = \OO_0\bar{\gamma} + \OO_0\ell^{e_\tau}$, which will be a cyclic left $\OO_0$-ideal of smooth norm $\ell^{e_\tau}$ equivalent to $I_\tau$.
- Compute the isogeny $\tau’$ corresponding to $J_{\tau}$ using
IdealToIsogenyFromKLPT()withend_close_to_E0 = True. The flag signals that $J_{\tau}$ is equivalent to an ideal of (relatively) small norm, which may causeEquivalentPrimeIdealHeuristic()to fail. Indeed, $J_{\tau} \sim I_{\tau}$ with $n(I_\tau) \simeq \sqrt[4]{p}$. To see more details on this, see the page Equivalent Prime Norm Ideals. - The secret key will then be the degree $n(J_\tau)$ isogeny $\tau’: E_0 \rightarrow E_A$ with corresponding public key $E_A$. We also return the (secret) ideals $I_{\tau}, J_{\tau}$ as these will be useful for future computations.
Commitment
To generate the commitment isogeny, we first generate a torsion basis $E_0[T’] = \langle P_0, Q_0 \rangle$. We then compute a secret integer $x$ and with this construct the kernel generator $K_\psi = P_0 + [x]Q_0$ such that $\psi : E_0 \to E_0 / \langle K_\psi \rangle = E_1$.
Next, by calling kernel_to_ideal(), we compute the ideal $I_{\psi}$ corresponding to the commitment isogeny $\psi: E_0 \rightarrow E_1$.
We keep as secret data the isogeny $\psi$ and the ideal $I_\psi$, and send as the codomain $E_1$ as our commitment to allow the generation of a challenge.
Challenge
The verifier receives $E_1$, the codomain of $\psi$, and computes the challenge isogeny kernel $\ker(\varphi)$ by computing a basis $E_1[D_c] = \langle P_1, Q_1\rangle$ and then computing a random kernel $\ker(\phi) = \langle P_1 + [x]Q_1\rangle$.
Response
The response is the most technical and slowest algorithm in the SQISign identification protocol. It runs as follows.
- Compute $\bar{I}_{\tau} \cdot I_{\psi} \cdot I_{\varphi}$ which corresponds to the isogeny $\varphi \circ \psi \circ \widehat{\tau}$. As $\ker(\phi) \not\in E_0$, computing $I_\phi$ is inefficient. Instead, the product $I_{\psi} \cdot I_{\varphi}$ can be computed directly from the intersection $I_{\psi} \cap I_{[\psi]^\star \phi} = I_{\psi} \cap I_{[\widehat{\psi}]_*\varphi}$. For more details on how this is done, see the page Pushforwards and Pullbacks. Then we run
multiply_ideals()on $\bar{I}_{\tau}$ and $I_{\psi} \cdot I_{\varphi}$ to obtain an ideal $I$. - Run
SigningKLPT()on $I$ to obtain a cyclic ideal $J \sim I$ of norm $\ell^e$, where $e$ is a fixed global parameter. See Estimating Bounds for KLPT for a discussion on how we set the size of $e$. Here, as $I$ is a left $\OO$-ideal where $\OO \neq \OO_0$, so we need to provide a connecting $(\OO_0, \OO)$-ideal as a second input. In this case, our second input is $J_{\tau}$. - We now want to find the isogeny corresponding to $J$. As $J$ is not a left $\OO_0$-ideal, we need to provide a left $\OO_0$-ideal whose right order is $\OO_L(J)$. By adjusting by an isomorphism if necessary, $J_{\tau}$ is such an ideal. Refer to the page Correct up to Isomorphism for more information on computing isomorphisms).
- Given the ideal $J, J_\tau$, we then calculate $\sigma$ as the isogeny corresponding to $J$ using
IdealToIsogenyFromKLPTwith $J_{\tau}$ and its corresponding isogeny $\tau’$ as additional input. - We compress the isogeny $\sigma$ as a bitstring $S$ using
compression, more information about the compression and following decompression is given on the page Modifying Compression.
The output of this algorithm is the bitstring $S$.
Verify
After decompressing the bitstring $S$ to obtain $\sigma$, the verification algorithm is a composition of the following checks:
- The codomain of $\sigma$ is isomorphic to $E_2$.
- The degree of $\sigma$ is $D = 2^e$.
- The isogeny $\widehat{\varphi} \circ \sigma$ is cyclic.
This last check is done by computing a torsion basis $E_A[2^f] = \langle P, Q \rangle$. The isogeny $\widehat\phi \circ \sigma$ is cyclic if and only if there are points in the image of this isogeny. It is enough to check $\widehat\phi \circ \sigma(P)$ and $\widehat\phi \circ \sigma(Q)$, and check if either has order $2^f$.
If all the checks pass, we return True. Otherwise, False.
Contents
We now give a short overview of the posts accessible on this website. The purpose of these posts is to highlight difficulties we encountered when implementing the algorithms above and explaining potential areas of confusion.
Background
- Working with Cyclic Ideals: in SQISign, we are interested in integral, cyclic ideals. We give an overview of these objects and how one can ensure a given ideal is cyclic.
- Correct up to Isomorphism: in many places, the Deuring correspondence is only correct up to isomorphism, but we must correct for exactness for the protocol to be successful. We discuss computing isomorphisms of ideals and isogenies.
- Pushforwards and Pullbacks: we describe how to compute the pushforwards and pullbacks of isogenies and ideals, which are vital for mapping to and from the curve $E_0$ with known endomorphism ring.
KLPT for SQISign
- Estimating Bounds for KLPT: we discuss how we can set heuristic bounds for the KLPT algorithm such that we have a high chance of success for each call of
EquivalentSmoothIdealHeuristic(). - Equivalent Prime Norm Ideals: one aspect of the KLPT algorithm requires computing equivalent prime norm ideals. This can fail on certain edge cases and this post aims to communicate how each edge-case is dealt with.
- Strong Approximation Lattice Trick: we can ensure the output of the KLPT has a small norm by using a lattice trick when solving the strong approximation. This page gives a detailed overview of how this works and how we have implemented it.
Computing isogenies from ideals
- Between Kernels and Ideals: at the core of the conversion of ideals and isogenies is the mapping between isogeny kernel generators and quaternion algebra generators of ideals. This page discusses how to implement the evaluation of endomorphisms $\alpha \in \BB$ on points $P \in E$ and then follows with a description of $\textsf{KernelToIsogeny}$ and $\textsf{IsogenyToKernel}$.
- Computing Isogenies from Ideals: we detail the algorithm that, given a cyclic ideal, computes the corresponding isogeny using
IdealToIsogenyFromKLPT(); the algorithm introduced in the SQISign paper which allows for the construction of a high-soundness identification protocol. - Subroutines when Computing Isogenies from Ideals: the above algorithm is complicated, and so to help readers, we factor out subroutines used in
IdealToIsogenyFromKLPT()into a separate page. - Meet in the Middle Isogenies: one step in the above algorithm is the brute force search of an $\ell^\Delta$ degree isogeny. We implement this with a meet in the middle algorithm using a depth-first search of the graph of j-invariants.
SQISign subtleties
- Small Steps from Curves with Small Endomorphisms: When we attempt to run the KLPT algorithm on an ideal which connects two left orders with particularly small norm, there is a chance the sub-algorithm to compute equivalent prime norm ideals may fail. This page gives detail on when we expect this to happen and how we pick an ideal filtration to ensure the protocol is successful.
- Modifying Compression: for our implementation, we found that we needed to include an additional bit to the compression algorithm to ensure successful decompression. This page details this bit, as well as giving a detailed discussion on the implementation of compression and decompression.
Conclusions
- Future Work: we summarise plans for future work, which are mainly focused between implementing the most modern description of SQISign following New algorithms for the Deuring correspondence: toward practical and secure SQISign signatures and the hope to improve the performance of isogeny computations in the current code.
Correspondence between notation
Due to the number of papers that have developed algorithms relating to the Deuring correspondence, there are various names out there for the same algorithm. Below we give a non-exhaustive list of equivalent names for algorithms in our code that appear in: the original SQISign paper; and Leroux’s thesis. We compare to these as they have associated implemented code.
| Our Code | SQISign | Leroux’s Thesis |
|---|---|---|
EquivalentSmoothIdealHeuristic | $\textsf{KLPT}_{l^*}$ | $\textsf{KLPT}_{\mathcal{N}}$ |
IdealToIsogenyFromKLPT | $\textsf{IdealToIsogeny}_{l^*}$ | $\textsf{IdealToIsogenyFromKLPT}_{l^*}$ |
IdealToIsogenySmallFromKLPT | $\textsf{IdealToIsogeny}_{l^{2f+\Delta}}$ | $\textsf{IdealToIsogenySmallFromKLPT}$ |
IdealToIsogenyCoprime | $\textsf{SpecialIdealToIsogeny}$ | $\textsf{IdealToIsogenyCoprime}_T$ |
Note that throughout our code, we add heuristic to the end of algorithm names to indicate when an algorithm with some (small) probability of failure, and therefore may have to be run $N$ times before terminating.